Log Number System for Low Precision Training

09 Oct, 2025

Introduction

Ok first things first, what is LNS? LNS stands for "Logarithmic Number System". So how does it store numbers and what it makes it different than storing numbers in FP32? Think of FP32 as a standard ruler where the markings and the distance between them is same throughout. The distance between 1 and 2 will be same as the distance between 10 and 11. But on the other side LNS is like a slide ruler where for smaller numbers the markings are extremely close and they get much further apart for large numbers. In this way the precision is high for numbers that are closer to 0 and it keeps on decreasing for numbers as they get bigger.

Example:

Let us store 9.5 in FP32

The number is broken down into 3 parts:

Sign: Positive or negative
Mantissa: These are the significant digits of the number. The binary of 9.5 is '1001.1'. In scientific notation this is written as '1.0011 *2^3'. The mantissa stores '0011' part.
Exponent: This will tell you how far you are supposed to float the binary point, here the exponent is 3.

Now let us store it in LNS It is way more direct. It also stores the sign but stores the log of the number's absolute value.

Sign: Is it positive or negative.
Logarithm: Calculates the base-2 log of the number. $l o g_{2} (9.5) \approx . 3.248$ So LNS system stores the sign and the single value 3.248 and the number is represented as

sign \times 2^{LogValue}

Now where does the difference lie? Like what did we accompolish by representing numbers differently? Is there any benefit.

Yes! speaking in terms of computational efficiency there is a lot of difference.

Let's say we want to multiply 8 by 16. In FP32:

Represent 8: $1.0 \times 2^{3}$ Represent 16: $1.0 \times 2^{4}$ To multiply:

Multiply the mantissas: $1.0 \times 1.0 = 1.0$ Add the exponents: $3 + 4 = 7$ Result: $1.0 \times 2^{7} = 128$ . This requires a dedicated, complex multiplication circuit.

In LNS:

Represent 8: $l o g_{2} (8) = 3$ Represent 16: $l o g_{2} (16) = 4$ To multiply: You just add the logarithmic values.

$3 + 4 = 7$ To get the result, you calculate $2^{7} = 128$ . The core operation is just an addition, which is much faster and more energy-efficient in hardware than multiplication.

Ok done with the basics, let us dig deep into this paper.

So if LNS is that good why aren't we using it right? Why isn't it the go to choice for al the AI hardware stuff? Well the answer is in the training of neural network and in the part of updating weights!

As mentioned earlier there is difference in the markings on the LNS scale right. This ever widening space between the numbers is called as 'quantization gap'. Imagine training an algorithm like SGD.

OK SGD 101:

Stochastic Gradient Descent (SGD): randomly pick one data point. Calculate error slope. Step opposite direction. Repeat many times. Update weights little by little. Faster than full data. Can jump out of traps (local minima). Gets model closer to best solution.

So in a nutshell, we make tiny changes to the weights of the model based on the errors we find. For a small weight the markings on our LNS scale are very close and precise so we will be able to register those easily without any problem and the update will be applied easily. But for larger weights the markings are miles apart and the system will be forced to choose the nearest available value which sometimes might lead it to select the same number thus resulting in no change to the weights of the network!

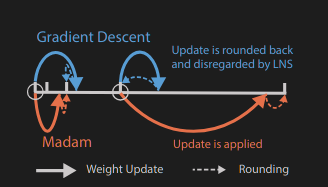
Udpating weights

This is the main crucial insight of the paper which states that 'updates generated by stochastic gradient descent (SGD) are disregarded more frequently by LNS when the weights become larger'.

What is the solution? Earlier methods used this weird hack to keep a second high precision FP32 copy of the weight just for the updates but this is stupid cause we are doubling the memory cost.

So the paper introduces a new framework to solve the above issue. In this both the number systsem and the learning algorithm are built to work around this issue.

A better "Multi Base" LNS:

Instead of having fixed pattern of marking the LNS-Madam team used "Multi-Base" LNS. A low base gives you high precision for smaller number and vice versa. Instead of choosing just one base LNS-Madam allows us to choose the best base for the job. This flexibility allows us to fine tune the precision of the system according to our needs ensuring that the quantization gaps are small as possible where it matters the most.

A Smart Optimizer - The "Madam" Optimizer

They basically went and replaced SGD with a more powerful tool: the Madam optimizer. So what is the difference? It is a multiplicative optimizer. So instead of updating the weights by increasing or decreasing them by 0.1 it makes them change by 1%. This change is absolutely genius because it solves our main problem entirely.

For a small weight change (e.g., 0.5)of 1% the reduction is tiny (-1.28) and the LNS tool is precise to handle it. But for a large weight (e.g. 128) the 1% reduciton is still a larger change (-1.28) and the update is now significant and easy to cross the qunatization gap. It doesn't get rounded away and gets applied successfully.